第37回の講座で、FFTによる振幅と位相の評価について解説した。今回は位相評価の注意点について述べる。

　まずはテストデータを作成しよう。原点を中心として左右対称のガウス関数を作成してほしい。wave の名前は、OrgWave、データ点数は128点、左右の値は-100と+100、線幅を 3 と設定しよう。Wave の scalingを忘れた人は、第13回の講座を復習すること。やり方は以下のコマンドの通り。

make/O/D OrgWave
setscale/I x -100, 100, “”, OrgWave
OrgWave=exp(-(x/3)^2)

wave が作成できたら、以下のようにグラフを作成し、正しくOrgWaveが作成できたか各自確認する事。

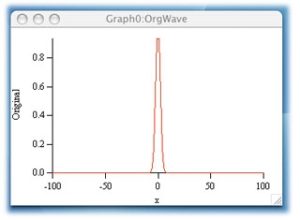
　続いてフーリエ変換だ。FFT “wave名”で、FFTが実行できるが、このコマンドではオリジナルデータに上書きされるので注意が必要だ。オリジナルのコピーとしてFFTwaveという名の wave を作成しておくと無難だろう。

Duplicate/O OrgWave FFTWave

FFT FFTwave

　位相の求め方も前回解説した。位相データは、以下のようにPhaseWaveという名の wave に格納するが、これは実数 wave なので まずredimension/R によって複素数型から実数型へ変換（再定義）する。位相データは、フーリエ変換したデータを直交座標から極座標へ変換したデータの虚数部で与えられるので、以下のように imag(), r2polar() を使えば求められるだろう。

duplicate/O FFTwave PhaseWave
redimension/R PhaseWave
PhaseWave=imag(r2polar(FFTWave))

　さらに前回解説した unwrap によって全位相が求められる。

unwrap 2*pi, PhaseWave

　これをグラフにすると以下のようになる。

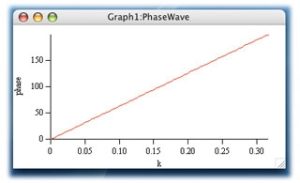
　これで完成と言いたいところだが、妙な結果にお気づきだろうか？ゼロ点を中心とするガウス関数を入力してフーリエ変換したにも関わらず、結果はゼロで一定ではなく、波数ベクトルに対して位相が線形になっている。これは特殊な補正が施されたFFTアルゴリズムを除いて、FFTプログラムに共通の問題点だ。理由は以下の通りだ。

　FFTを行うデータは、yWave 対 xWave のデータセットではなく、スケーリングされた yWave 自身であることは先に述べた。今回の場合、データのレンジは-100から+100である事をIGORに告げ、その結果 x 軸の間隔は１から (100-(-100))/127=1.5748 に変更された。FFTは、後者のデータ間隔を考慮してFFTを実行するが、-100から+100にスケーリングされている事を知らない（理解できない）。説明を加えると、FFTは、-100 から+100に対して実行されるのではなく、0 から 200に対して実行されるのだ。皆さんご存じの通り、FFTの「大きさ」については何ら影響を与えないが、正しい位相評価はこのままでは行えない。そこで、これまで通りにFFTを実行し、この効果を補正する方法について解説する。

　f(x)のフーリエ変換がF(k)であるとき、f(x+a)のフーリエ変換はF(k)exp(ika)なので、通常通りF(k)を求め、実数および虚数部にそれぞれcos(ka)とsin(ka)をかければ位相のズレは補正できる。以下のコードを実行して正しい位相を求めてみよう。上書きをさけるため、Corrを加えたwave名を付けた。

duplicate/O FFTwave FFTwaveCorr
FFTwaveCorr*=cmplx(cos(-100*2*pi*x), sin(-100*2*pi*x))
duplicate/O FFTwaveCorr PhaseWaveCorr
redimension/R PhaseWaveCorr
PhaseWaveCorr=imag(r2polar(FFTWaveCorr))
unwrap 2*pi, PhaseWaveCorr

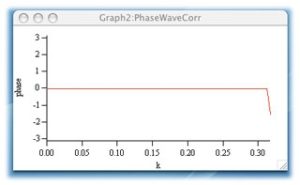
いかがだろろうか。上のグラフは-πから+πの範囲でプロットしたが、kはほぼ一定の値をとるようになった。グラフの右端のドロップは、データ末端の効果で、これも補正可能だ。これについては後日回避方法を解説する。