当研究室では、光・中性子・Ｘ線を使った散乱実験はもちろん、種々の顕微鏡画像データの解析に対してもこれらと等価な散乱関数を駆使した解析を行っている。「光散乱」や「フーリエ変換」と言う言葉を聞いて避けたがる学生さんも多いが、周期性の定量化や数学的利便性の観点から、これらは理工系のデータ解析において必要不可欠な技術だ。

いわゆる散乱屋にとっては、実空間と逆空間を行き来することは何の苦労も伴わない簡単な操作だが、これからFFTにチャレンジする学生さんにはまずとっかかりが欲しいところだろう。FFTを理工系の道具として使うために、数学的観点だけではなく、物理的観点で解説したいのはやまやまだが、これは後日IGOR Pro講座とは別に機会があれば解説したい。

今日はひとまず「画像の特徴（構造）」を表す１次元のスペクトルを作成し、これに２次元のランダムノイズパターンを作成して、多彩なパターンを作成してしてみよう。まずは興味をもってもらうところからはじめる事が大事なので、これらが学生さんの散乱やFFTの理解の糸口となるように望んでいる。

Function Spec1D(qq, kk,vv, rr)
variable qq
variable kk
variable vv
variable rr
variable Sq=1/(kk*qq^4+vv*qq^2+rr)
return Sq
end

■WindowsメニューからProcedure Windowを開き、上記のようなFunction を作成しよう。この１次元散乱関数を後ほど２次元に拡張する。

■入力が済んだらウインドウを閉じ、コマンドラインに移って下記のコマンドを入力していこう。

Make/O/N=(512,512)/D SimuSpecImage
Make/O/D/N=256 yy,xx
xx=p/255*512/2/500*2*pi
yy=Spec1D(xx, 1,0.05, 0.001)

SimuSpecImage は、二次元画像データを格納するための wave だ。後ほど使う。yy および xx は特に画像変換とは関係ないが、作成した１次元スペクトルを確認するために作成してみよう。xx の実際のスケールとして 500nm を設定している。必要とあらば他の値に変更しても良い。スケールを２で割るのはナイキスト周波数を考慮しての事。さらに余談だが、小角散乱屋は２πをつけるが、Ｘ線回折屋さんは、それをつけない。逆変換のときの対応関係にさえ気を付ければよい。p 関数については第４回の講座を参照のこと。yy と xx に対してプロットすると、以下のようなグラフが得られるはずだ。

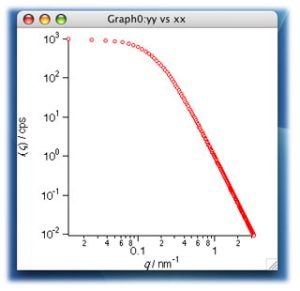
■次に画像データとなる SimuSpecImage についても準備を進めよう。

setscale/I x (-512/2/500*2*pi), (512/2/500*2*pi), “”, SimuSpecImage
setscale/I y (-512/2/500*2*pi), (512/2/500*2*pi), “”, SimuSpecImage
SimuSpecImage=Spec1D((x^2+y^2)^0.5, 1,0.05, 0.001)

setscaleコマンドはもう何度も登場しているので、説明は不用だろう。また、上で作成した１次元散乱関数を (x, y) の関数として二次元スペクトルに拡張できる。

■上で作成した構造を表すスペクトルに対して、ランダム方向のノイズを加えて（第６回）逆変換する事で構造パターンを作成してみる。以下のコマンドをどんどん実行していただきたい。

Duplicate/O SimuSpecImage SimuNoise
SimuNoise=gnoise(pi)
Duplicate/O SimuNoise SimuNoiseTemp
Redimension/C SimuNoise
SimuNoise=cmplx(cos(SimuNoiseTemp),sin(SimuNoiseTemp))
KillWaves SimuNoiseTemp
Redimension/C SimuSpecImage
SimuSpecImage*=SimuNoise

Redimension は wave の種類を変更する命令で、（１）変数・テキストに加えて、（２）単精度・倍精度配列や（３）実数・虚数の切り替えが可能だ。ここでは /C オプションにより一旦データを複素数にして様々な位相ノイズを加えている。WindowsメニューからNew, さらに Image Plot…を選ぶと、次のようなSimuSpecImage の画像データが表示できるはずだ。

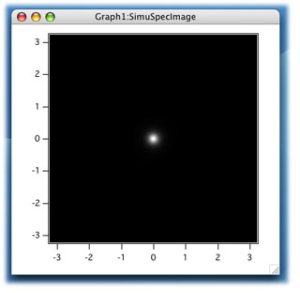
IGOR Proもどんどん便利になり、もはや自分でFFTルーチンを作成する必要はなくなってしまった。いくつかのオプションに関する注意点はあるものの、基本的にはコマンドラインでFFTを実行するだけでフーリエ変換が行える。コマンドラインで以下の命令を実行していこう。

FFT SimuSpecImage
SimuSpecImage=SimuSpecImage*conj(SimuSpecImage)
Redimension/R SimuSpecImage
SimuSpecImage=(SimuSpecImage^0.5)/4
setscale/I x 0, 500, “”, SimuSpecImage
setscale/I y 0, 500, “”, SimuSpecImage

デフォルトのFFTは場の変換であるために出力は複素数である。conj 関数によって複素共役をかけ二乗振幅に変換し、再度 Redimension 命令によって実数 wave に変換する。この二次元フーリエ変換は、変換元として複素数 wave を用意しておかないと（虚数部なしの）片面変換となる事が注意点だ。画素数に依存する強度補正や画像スケールの補正の後、以下のような画像パターンが出現すれば成功だ。

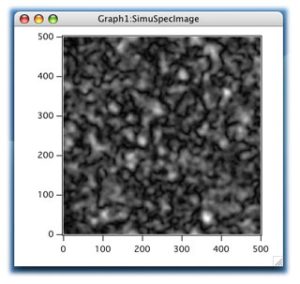
ちなみに、最初の散乱関数で vv のみを負にすると（例えば、vv – -0.05）、スペクトルはリングとなり、高度な周期性を示す。この変換画像は以下のようになる。

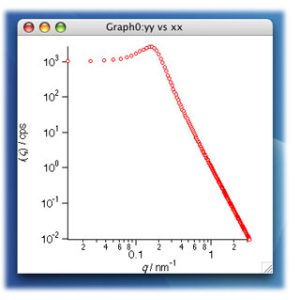
難しい理論を一切説明しないのがいい事なのかは疑問だが、フーリエ変換を使ってできる事、IGOR Proを使ってできること、散乱空間と実際の空間は何かしらの関係で結びつけられることが感じ取れたのではないだろうか。